小中学生の時、勉強が得意だったが高校に入った途端勉強ができなくなってしまった。あるいは、その逆で高校に入ってから得意になったり、大学に入ってから興味のある分野を勉強するようになり、その結果成績が良いなどという人がいると思います。
私は小学生の時は比較的勉強が得意で、中学受験をして地元ではない中高一貫校に進学しました。当時は本当に合格したくて、めちゃくちゃ勉強しました。ただその勉強法では、中学に入ってからすぐに挫折しました。ただガムシャラにただただ勉強していたからです。
こういうタイプの人は比較的多いと思います。勉強は好きで勉強はしているんだけれども、ノートに単語をまとめるだけであったり、語呂合わせで試験を乗り切ったり、、、また私は数学が得意なつもりでした。試験前に試験範囲を2周して、類題だけをとけばほぼ9割取れる。。。
こういう試験前にやっていた勉強法で勉強する癖が身についてしまって、大学受験ではかなり苦労した思い出があります。
私は理系の大学に通っていますが、大学入試は直前まで「初見の問題が全く解けない」という悩みを抱えておりました。今までちゃんと勉強してきたつもりなのに全然手が出ないのです。典型的な例題レベルであれば解けるのですが、ちょっと捻った問題だと手につきません。
中学受験で成功した私は努力は必ず報われると信じていたため、ガムシャラに勉強しました。ただ、直前で気づいたのです。例題をこなす勉強法では合格できないと
そこからは、ある程度基礎力がついているわけですから、どのように初見の問題を考えて行くかということにフォーカスをあてて受験勉強をしていました。するとどうでしょう、成績がどんどん上がっていくのです。
数学の本質はただ類題を解けることではありません。ちゃんと定義に戻り、どのように考えていけばいいか自分なりに考察していくことが大事です。
初見の問題を解くときは設定をまず確認することが大事です。与えられているものは何か(仮定)。最終的に何を導き出せば良いのか(答え)。そのためにどのような考え方をすればよいのか(プロセス)。をちゃんと意識しましょう。
中学受験の問題を例にあげましょう
1個80円のりんごと1個50円のみかんをあわせて11個買ったら、代金は700円でした。
みかんは何個買いましたか?
ガムシャラに勉強してきた受験生は「塾で習った面積図を使えばいいんだ!」
こういう風に思って解答をスラスラと書きます。
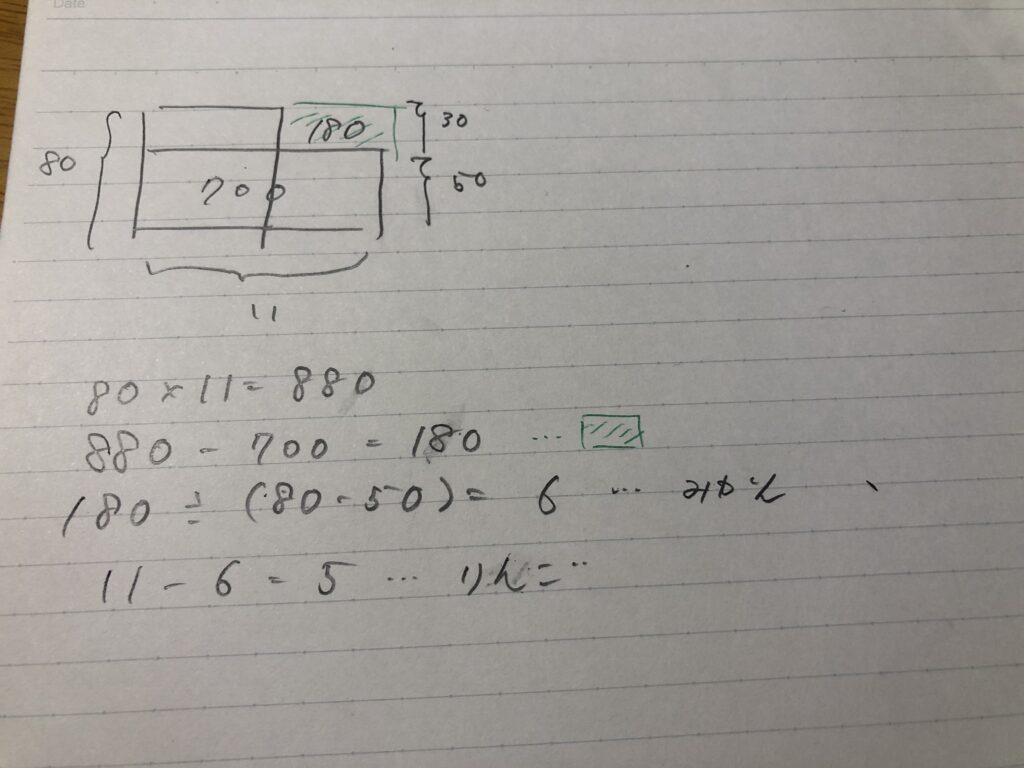
でもどうでしょうか、本当にやり方の丸暗記で終わらせていいものでしょうか。
なぜ面積図を使うのか、という点に着目しなければ伸びません。
つまり、面積図は11個分を全てどちらか一方にしてしまう。そこから差分を考えていくという考え方ですよね。
このように教わっている人と、教わっていない人がいることは事実です。しかしながら教わっていても自分でよく考えられない子、教わっていなくても考えられる子がいることも事実です。
どちらかに個数を揃えて考えるというように問題をもう少し抽象化すればあらゆる場面で応用が効くはずです。
抽象化するためにどうしてこのように考えたかを意識することが大事です。そのため、幼少期からなぜ?と疑問を持つ癖をつけましょう。
解いているときになぜこうといたのか質問してみてください。
抽象化をしつつ、具体例で思考のプロセスを踏めばあらゆる問題にチャレンジできるようになります。
丸暗記の勉強より楽しいはずです。
コメント欄でコメントいただけると幸いです。